『ばね振り子の力学的エネルギー』の『このように』で説明しましたが、鉛直ばね振り子においては、「自然長の位置」でなく「つり合いの位置」を中心とみなすと重力について考えなくてすみます。斜面上のばねについても同じです。
つり合いの位置、点P0を位置エネルギーの基準点とし、この地点での物体の速さを v0 とします。
すると、点P0での力学的エネルギーは \(\large{\frac{1}{2}}\)mv02 で、
スタート地点(最高地点)での力学的エネルギーは \(\large{\frac{1}{2}}\)kx2 で、
力学的エネルギー保存の法則より、
\(\large{\frac{1}{2}}\)mv02 = \(\large{\frac{1}{2}}\)kx2
であり、(この式は『鉛直ばね振り子の力学的エネルギー』の『各点でのおもりの速さ』の『O'点でのおもりの速さ』の式に相当します)
速さは
v02 = \(\large{\frac{k}{m}}\)x2
∴ v0 = \(\sqrt{\large{\frac{k}{m}}}\) x
と求められます。
(別解:自然長の位置を基準とした場合の方法も一応示しておきます)
 x だけ引き上げた地点(最高点)での力学的エネルギーを考えてみますと、
x だけ引き上げた地点(最高点)での力学的エネルギーを考えてみますと、
・運動エネルギーは 0
・弾性エネルギーは \(\large{\frac{1}{2}}\)k(x - x0)2
・位置エネルギーは mg(x - x0)sinθ
よって力学的エネルギーは 0 + \(\large{\frac{1}{2}}\)k(x - x0)2 + mg(x - x0)sinθ ……①
(これは『鉛直ばね振り子の力学的エネルギー』のA点での力学的エネルギーに相当します)
 点P0での力学的エネルギーを考えてみますと、
点P0での力学的エネルギーを考えてみますと、
・運動エネルギーは \(\large{\frac{1}{2}}\)mv02
・弾性エネルギーは \(\large{\frac{1}{2}}\)kx02
・位置エネルギーは mg(- x0)sinθ
よって力学的エネルギーは \(\large{\frac{1}{2}}\)mv02 + \(\large{\frac{1}{2}}\)kx02 + mg(- x0)sinθ ……②
(これは『鉛直ばね振り子の力学的エネルギー』のO'点での力学的エネルギーに相当します)
力学的エネルギー保存の法則より ①式 = ②式。つまり、
\(\large{\frac{1}{2}}\)k(x - x0)2 + mg(x - x0)sinθ = \(\large{\frac{1}{2}}\)mv02 + \(\large{\frac{1}{2}}\)kx02 + mg(- x0)sinθ
∴ \(\large{\frac{1}{2}}\)k(x - x0)2 + mgxsinθ = \(\large{\frac{1}{2}}\)mv02 + \(\large{\frac{1}{2}}\)kx02
∴ \(\large{\frac{1}{2}}\)kx2 - \(\large{\frac{1}{2}}\)2kxx0 + \(\large{\frac{1}{2}}\)kx02 + mgxsinθ = \(\large{\frac{1}{2}}\)mv02 + \(\large{\frac{1}{2}}\)kx02
∴ \(\large{\frac{1}{2}}\)kx2 - kxx0 + mgxsinθ = \(\large{\frac{1}{2}}\)mv02 問1の kx0 = mgsinθ を代入して
∴ \(\large{\frac{1}{2}}\)kx2 - mgxsinθ + mgxsinθ = \(\large{\frac{1}{2}}\)mv02
∴ \(\large{\frac{1}{2}}\)kx2 = \(\large{\frac{1}{2}}\)mv02
∴ v0 = \(\sqrt{\large{\frac{k}{m}}}\) x
と同じ結果が得られます。(大変な労力です)
 物体は点P0を中心として振幅 x の単振動をするから、自然長からの最大の伸びは
物体は点P0を中心として振幅 x の単振動をするから、自然長からの最大の伸びは
x0 + x
(運動方程式 ma = F を立てて a を求める)
この位置での物体の加速度を a と置きます。
この位置での加速度は 0 ではありません。
一瞬物体の動きは止まりますが、それは速度が 0 なのです。
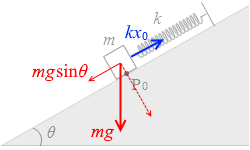
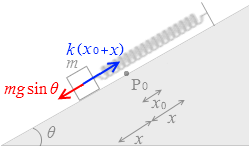 物体にはたらく力は左下方向を正として、
物体にはたらく力は左下方向を正として、
mgsinθ - k(x0 + x)
よって運動方程式は
ma = mgsinθ - k(x0 + x)
であり、問1の kx0 = mgsinθ を代入すると、
ma = mgsinθ - mgsinθ - kx
∴ ma = - kx
∴ a = - \(\large{\frac{k}{m}}\) x
これは左下方向を正とした場合の加速度であり、問題は加速度の大きさを聞いているので、
a = \(\large{\frac{k}{m}}\) x
 x だけ引き上げた地点(最高点)での力学的エネルギーを考えてみますと、
x だけ引き上げた地点(最高点)での力学的エネルギーを考えてみますと、 点P0での力学的エネルギーを考えてみますと、
点P0での力学的エネルギーを考えてみますと、 物体は点P0を中心として振幅 x の
物体は点P0を中心として振幅 x の 物体にはたらく力は左下方向を正として、
物体にはたらく力は左下方向を正として、