図3のように、軽い糸でつながった、質量 M の物体Aと質量 m の物体Bが、なめらかな水平面上に置かれている。物体Aに一定の大きさ F の力を水平方向に加え、全体を等加速度運動させる。ただし、糸は水平であるものとする。
（問3）物体Aと物体Bをつなぐ糸の張力の大きさを式で表わせ。
（問4）qI2QB
#センター17本試物理基礎
図3のように、軽い糸でつながった、質量 M の物体Aと質量 m の物体Bが、なめらかな水平面上に置かれている。物体Aに一定の大きさ F の力を水平方向に加え、全体を等加速度運動させる。ただし、糸は水平であるものとする。
（問3）物体Aと物体Bをつなぐ糸の張力の大きさを式で表わせ。
（問4）qI2QB
#センター17本試物理基礎
（問3）
張力を T と置きます。張力はどこもかしこも同じ大きさなので物体Aに掛かる張力と物体Bに掛かる張力は同じ大きさです。
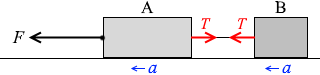また、加速度を a と置きますと、これも物体Aと物体Bで共通です。糸でつながっているのですから。
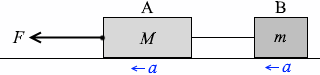物体A、物体B全体の運動方程式を立てますと、
(M + m)a = F ……①
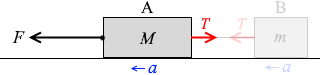物体Aの運動方程式を立てますと、
Ma = F - T ……②
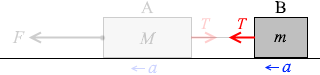物体Bの運動方程式を立てますと、
ma = T ……③
3つの式のうちどれか2つを使うと a が消去できます。一番計算が楽なのは③式を①式に代入する方法です。
③式を変形して、
a = \(\large{\frac{T}{m}}\)
①式に代入して、
(M + m)\(\large{\frac{T}{m}}\) = F
∴ T = \(\large{\frac{m}{M+m}}\)F