図1のように、鉛直な壁面、半径 R の円筒面、水平な天井面がなめらかにつながっている。質量 m の小物体を点Oから速さ v0 で鉛直上方に打ち出したところ、小物体は距離 h だけ壁面に沿って運動した後、円筒面に沿って運動し、点Aを通過した。ただし、すべての面はなめらかであるものとする。また、重力加速度の大きさを g とする。
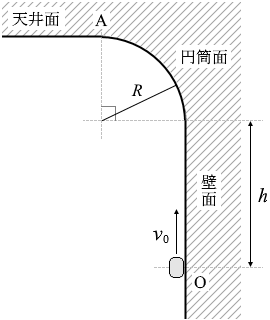
(問1)小物体が点Aを通過するときの速さ vA を式で表わせ。
(問2)小物体が点Aを通過するための、vA の最小値を式で表わせ。
#センター16本試物理
図1のように、鉛直な壁面、半径 R の円筒面、水平な天井面がなめらかにつながっている。質量 m の小物体を点Oから速さ v0 で鉛直上方に打ち出したところ、小物体は距離 h だけ壁面に沿って運動した後、円筒面に沿って運動し、点Aを通過した。ただし、すべての面はなめらかであるものとする。また、重力加速度の大きさを g とする。

(問1)小物体が点Aを通過するときの速さ vA を式で表わせ。
(問2)小物体が点Aを通過するための、vA の最小値を式で表わせ。
#センター16本試物理
(問1)
点Oでの小物体の力学的エネルギーは
(運動エネルギー)+(位置エネルギー)= \(\large{\frac{1}{2}}\)mv02 + 0
点Aでの小物体の力学的エネルギーは
(運動エネルギー)+(位置エネルギー)= \(\large{\frac{1}{2}}\)mvA2 + mg(R+h)
\(\large{\frac{1}{2}}\)mv02 + 0 = \(\large{\frac{1}{2}}\)mvA2 + mg(R+h)
∴ v02 = vA2 + 2g(R+h) ……①
∴ vA2 = v02 - 2g(R+h)
∴ vA = \(\sqrt{{v_0}^2-2g(R+h)}\)
(問2)
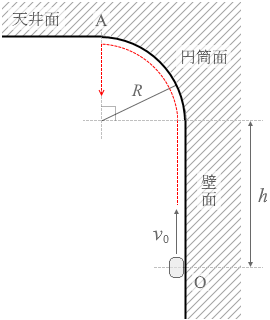 もし、点Aで静止し、その後真下に落下するのであれば、運動エネルギーが 0 であるとして力学的エネルギー保存の法則の式を立てて簡単に求められそうですが、そのようなことは起こりません。小物体の運動の軌跡はなだらかな曲線になります。物にぶつかったりしないかぎり急に向きを変えるような動きはしません。
もし、点Aで静止し、その後真下に落下するのであれば、運動エネルギーが 0 であるとして力学的エネルギー保存の法則の式を立てて簡単に求められそうですが、そのようなことは起こりません。小物体の運動の軌跡はなだらかな曲線になります。物にぶつかったりしないかぎり急に向きを変えるような動きはしません。
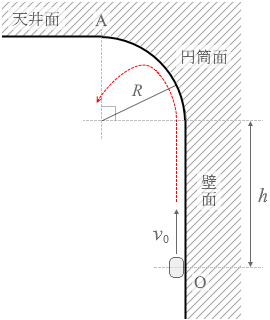 スピードが足りない場合はこんな感じで、
スピードが足りない場合はこんな感じで、
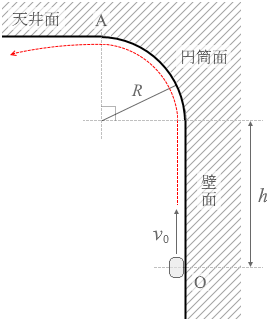 スピードが十分ならこんな感じになります。
スピードが十分ならこんな感じになります。
ではどのように考えればいいかというと、それは円軌道であることに着目し円運動の運動方程式を立てるのです。
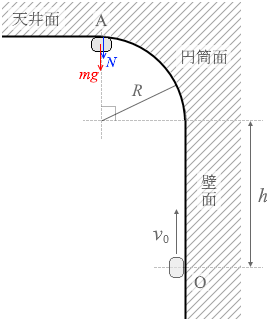 点Aにおいて小物体にはたらいている力は、重力 mg と垂直抗力 N で、これらの力が円運動の向心力となっています。つまり、
点Aにおいて小物体にはたらいている力は、重力 mg と垂直抗力 N で、これらの力が円運動の向心力となっています。つまり、
m\(\large{\frac{{v_A}^2}{R}}\) = mg + N
であり、変形すると、
N = m\(\large{\frac{{v_A}^2}{R}}\) - mg
であり、N ≧ 0 であれば、小物体は垂直抗力を受けているということであり、面に接触している、すなわち点Aを通過するということになります。
というわけで、
N = m\(\large{\frac{{v_A}^2}{R}}\) - mg ≧ 0
∴ m\(\large{\frac{{v_A}^2}{R}}\) ≧ mg ……②
∴ vA2 ≧ gR
∴ vA ≧ \(\sqrt{gR}\)
よって、vA の最小値は \(\sqrt{gR}\) です。
(別解)
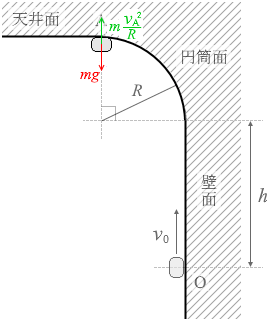 遠心力の大きさは向心力の大きさと同じであり、m\(\large{\frac{{v_A}^2}{R}}\) です。そしてこれが mg 以上の大きさであれば小物体は面と接触し続ける、と考えて、いきなり②式
遠心力の大きさは向心力の大きさと同じであり、m\(\large{\frac{{v_A}^2}{R}}\) です。そしてこれが mg 以上の大きさであれば小物体は面と接触し続ける、と考えて、いきなり②式
m\(\large{\frac{{v_A}^2}{R}}\) ≧ mg
を立ててもいいです。
(余談1)
問2の答えを問1の①式に代入してみますと、
v02 = vA2 + 2g(R+h)
⇔ v02 = gR + 2g(R+h)
∴ v02 = g(3R+2h)
∴ v0 = \(\sqrt{g(3R+2h)}\)
(余談2)
宙返りジェットコースターの最上点でのスピードも \(\sqrt{gR}\) 以上の値になっています。