単振り子の力学的エネルギー

単振り子

糸の一端を固定し、他端におもりを付けて吊るし、重力の作用で鉛直面内を振らせたものを単振り子といいます。＊糸は伸び縮みせず、質量が無いものとします。質量があると、糸の運動エネルギーや位置エネルギーを考慮しなければならず、問題が複雑になってしまいます。質量があるのはおもりだけです。

また、糸もおもりも空気抵抗を受けないものとします。

「単振り子」の「単」は、たぶん「１つ」という意味だと思います。あるいは「単純」の「単」かもしれません。おもりが１つで鉛直面内で運動する単純な振り子が単振り子です。
おもりが２つある振り子は二重振り子といいます。とても複雑な動きをします。高校物理では扱いません。他に、円錐振り子、球面振り子などというものもあります。
　閉じる

本項では、単振り子のおもりの各瞬間の速さが力学的エネルギー保存の法則によって求められるという話をします。

単振り子を微小振動させてその周期などを求める話は『単振り子』項でします。

振り子の張力は仕事をしない

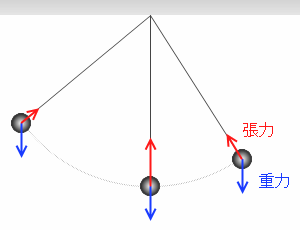振り子の運動では糸に張力がはたらきます。この張力はおもりの運動方向と常に垂直の方向を向いているので、おもりに対して仕事をしません。すなわち、おもりのエネルギーの増減に関わりません。力学的エネルギーに無関係なのです。

振り子のおもりには、糸の付け根方向の張力と、鉛直下向きの重力の2つの力がはたらきますが、力学的エネルギーに関しては、張力は考える必要はなく重力のみを考えます。重力は保存力であるので力学的エネルギー保存の法則が成り立ちます。

おもりの速さを求める

力学的エネルギー保存の法則を使って、単振り子のおもりの速さを求めてみます。

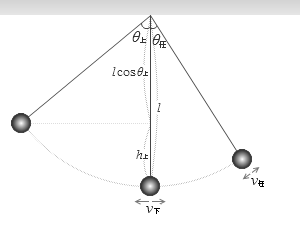長さ l [m] の軽い糸に、質量 m [kg] のおもりを付けた単振り子があるとします。このおもりを最下点から高さ h_上 [m] の最上点の位置＊最上点というのは手を放す位置、つまりスタート地点という意味です。天井と同じ高さの位置というわけではありません。
　閉じるで静かに放したときのおもりの速さを求めます。重力加速度の大きさを g [m/s²] とし、空気抵抗は無視できるものとします。

＊高さについて：上図を見てもらうとわかると思いますが　h = l - l cosθ = l (1-cosθ)　です。

力学的エネルギー保存の法則により、常に　E_上 = E_任 = E_下　です。

最上点でのおもりの力学的エネルギーと速さ

自由落下運動のときのように力学的エネルギーを考えてみます。

E_上 = K_上 + U_上 = 0 + mgh_上 = mgh_上 = mgl (1 - cosθ_上)

最上点でのおもりの速さは v_上 = 0 です。振り子のおもりは最上点では一瞬止まるので 0 です。

任意の位置でのおもりの力学的エネルギーと速さ

E_任 = K_任 + U_任 = \(\large{\frac{1}{2}}\)mv_任² + mgh_任 = \(\large{\frac{1}{2}}\)mv_任² + mgl (1 - cosθ_任)

力学的エネルギー保存の法則より E_上 = E_任 だから、

　　　mgl (1 - cosθ_上) = \(\large{\frac{1}{2}}\)mv_任² + mgl (1 - cosθ_任)

∴　　mgl (1 - cosθ_上) - mgl (1 - cosθ_任) = \(\large{\frac{1}{2}}\)mv_任²

∴　　- mgl cosθ_上 + mgl cosθ_任 = \(\large{\frac{1}{2}}\)mv_任²

∴　　mgl cosθ_任 - mgl cosθ_上 = \(\large{\frac{1}{2}}\)mv_任²

∴　　mgl (cosθ_任 - cosθ_上) = \(\large{\frac{1}{2}}\)mv_任²

∴　　2gl (cosθ_任 - cosθ_上) = v_任²

∴　　v_任 = \(\sqrt{2gl(\cos\theta_任 - \cos\theta_上)}\)

これを θ_上 を使わず、h_上 を使って表現してみます。
h_上 = l (1-cosθ_上)　 より 　h_上 = l - lcosθ_上　 よって 　h_上 - l = - lcosθ_上　 であり、これを上式に代入しますと、

　　　v_任 = \(\sqrt{2gl(\cos\theta_任 - \cos\theta_上)}\)

　　　　 = \(\sqrt{2g(l\cos\theta_任 - l\cos\theta_上)}\)

　　　　 = \(\sqrt{2g(l\cos\theta_任 + h_上 - l)}\)

　　　　 = \(\sqrt{2g(h_上 - l + l\cos\theta_任)}\)

　　　　 = \(\sqrt{2g\{h_上 - l(1 - \cos\theta_任)\}}\)

最下点でのおもりの力学的エネルギーと速さ

E_下 = K_下 + U_下 = \(\large{\frac{1}{2}}\)mv_下² + 0 = \(\large{\frac{1}{2}}\)mv_下²

力学的エネルギー保存の法則より E_上 = E_下 だから、

　　　mgl (1 - cosθ_上) = \(\large{\frac{1}{2}}\)mv_下²

∴　　2gl (1 - cosθ_上) = v_下²

∴　　v_下 = \(\sqrt{2gl(1 - \cos\theta_上)}\)

E_上 は mgl (1 - cosθ_上) であると同時に mgh_上 でもあるので、 E_上 = E_下 は以下のようにも表せます。

　　　mgh_上 = \(\large{\frac{1}{2}}\)mv_下²

∴　　2gh_上 = v_下²

∴　　v_下 = \(\sqrt{2gh_上}\)　＊上式に　h_上 = l (1-cosθ_上)　を代入したものと考えることもできます。

θ_上 を使わず、h_上 を使って表現したということです。
　閉じる

このように

力学的エネルギー保存の法則を使うことにより、単振り子のおもりの速さが求められます。

なお、文中で θ_上 や v_下 などという表記を用いましたが、これはわかりやすくするためであり、物理の数式表記の慣習には反します。答案用紙に解答を書く際は、このような記号は用いず、θ'、 v₀ などと表記してください。また、問題文中の記号が上記の記号のどれに当てはまるのか、たとえば問題文中で θ が出てきた時、上記のうちの θ_上 なのか θ_任 なのか θ_下 なのか、どれに当てはまるのか慎重に考えてください。それらに気を付ければ上記の式のうちいずれかを使って問題を解くことができるはずです。

たとえば

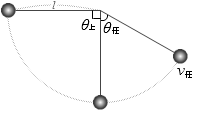単振り子の支点と同じ高さまでおもりを持ち上げて放したとき、角度60°の地点でのおもりの速さは？と問われたら、

v_任 = \(\sqrt{2gl(\cos\theta_任 - \cos\theta_上)}\)　の式を使えば求まります。

θ_任 = 60°、θ_上 = 90° を代入すると、

　　　　v_60° = \(\sqrt{2gl(\cos\theta_任 - \cos\theta_上)}\)

　　　　　　 = \(\sqrt{2gl(\cos60° - \cos90°)}\)

　　　　　　 = \(\sqrt{2gl(\frac{1}{2} - 0)}\)

　　　　　　 = \(\sqrt{gl\ }\)

さらに、このときの最下点でのおもりの速さは？と問われたら、

θ_任 = 0°、θ_上 = 90° を代入して、

　　　　v_0° = \(\sqrt{2gl(\cos\theta_任 - \cos\theta_上)}\)

　　　　　　 = \(\sqrt{2gl(\cos0° - \cos90°)}\)

　　　　　　 = \(\sqrt{2gl(1 - 0)}\)

　　　　　　 = \(\sqrt{2gl}\)

これは　v_下 = \(\sqrt{2gh_上}\)　に　h_上 = l　を代入しても求まります。

逆に、最下点で初速を与えたとき、おもりがどのくらいの高さまで持ち上がるかを問われたら、 2gh_上 = v_下²　の式に　v_下　の値を代入すれば　h_上　が求まります。高さでなく角度を問われたなら、 2gl (1 - cosθ_上) = v_下²　の式に代入すれば求まります。