共振回路

RLC直列回路における周波数と電流

RLC直列回路において交流電源の周波数を変化させたとき、流れる電流はどうなるか、考えてみます。

電流を大きくするには

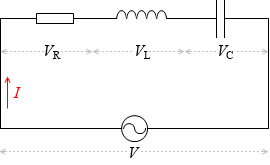『RLC直列回路』項で説明したように、直列回路においては３つの部品に流れる電流は同じで、全体の電圧（交流電源の電圧）は３つの部品の各電圧の和です。

交流の大きさ（実効値）が決っている電源を用いたとき、その電圧は３つの部品に分配されるわけです。

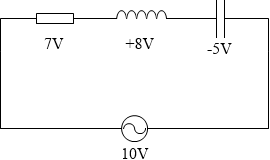たとえば電源が 10V のとき、抵抗が +7V、コイルが +8V、コンデンサーが -5V というような具合です。

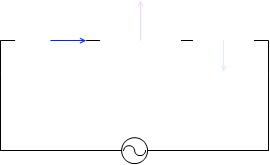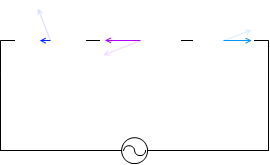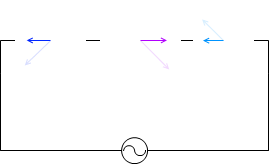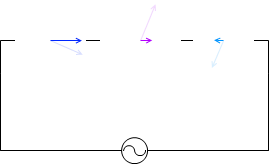『RLC直列回路』項で説明したように、電圧の位相について、コイルは抵抗に比べて \(\large{\frac{π}{2}}\) 進んでいて、コンデンサーは抵抗に比べて \(\large{\frac{π}{2}}\) 遅れているので、コイルとコンデンサーは位相が π ズレています。位相が π ズレているということは常に正負が逆向きということです。

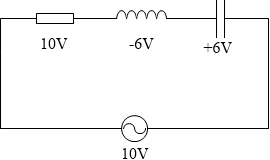ですので、コイルとコンデンサーの電圧の大きさが同じであれば常に互いに打ち消し合います。そして電源の電圧と抵抗の電圧が等しくなります。

たとえば電源が 10V のときに抵抗が +10V、コイルが -6V、コンデンサーが +6V というような具合です。

コイルの電圧とコンデンサーの電圧を同じにできれば、抵抗の電圧を電源の電圧にまで高めることができます。

ω によって調整可能

このときにコイルの自己インダクタンス L の値やコンデンサーの電気容量 C の値が決っていると、コイルやコンデンサーに掛かる電圧も決まってしまうのではないかと思いきや、これらは ω の大きさによって調整が可能です。

コイルに掛かる電圧を実効値を使って表すと、

　　　　V_Le = ωLI_e

コンデンサーに掛かる電圧を実効値を使って表すと、

　　　　V_Ce = \(\large{\frac{I_\rm{e}}{ωC}}\)

I_e、L、C の値が決まっていても ω 次第でこの２式を等しくすることができます。上式は ω が大きくなると大きくなり、下式は ω が大きくなると小さくなり、ちょうどいい頃合いを探すと両式を等しくすることができます。

　　　　ωLI_e = \(\large{\frac{I_\rm{e}}{ωC}}\)

　　∴　 ωL = \(\large{\frac{1}{ωC}}\)　　……①

　　∴　 ω² = \(\large{\frac{1}{LC}}\)

　　∴　 ω = \(\large{\frac{1}{\sqrt{LC}}}\)

共振周波数

ω がこのような値のときに V_Le = V_Ce になり、コイルとコンデンサーの電圧が互いに打ち消し合い、電源と抵抗の電圧が等しくなります。この大きさのときの ω を共振角周波数といい ω₀ で表します。

角周波数 ω を周波数 f で表すと f = \(\large{\frac{ω}{2π}}\) という関係がありますから f₀ = \(\large{\frac{ω_0}{2π}}\) = \(\large{\frac{1}{2π\sqrt{LC}}}\) となり、この f₀ を共振周波数といいます。この値は『振動回路』項の固有周波数と同じ値になっています。

交流電源の周波数が共振周波数であるとき、コイルの電圧とコンデンサーの電圧が打ち消し合い、電源の電圧がすべて抵抗に掛かります。抵抗に掛かる電圧が最大になるのです。電圧が最大ということは、オームの法則 I = \(\large{\frac{V}{R}}\) より、電流も最大になります。直列回路では電流の大きさは各地点で同じなので、抵抗の電流が最大のときは回路に流れる電流も最大です。つまり、RLC直列回路で交流電源の周波数が共振周波数であるとき、回路に最大の電流が流れます＊交流電流は大きさが絶えず増減しているわけですが、その範囲の中で最大という意味ではなく、交流電流の最大値や実効値が最大、ということです。
　閉じる。

L や C の値は回路ごとに決まっていますので、共振周波数の値は回路固有の値です。回路ごとに決まった値です。共振周波数の電流が回路に流れることを共振するといい、その状態の回路を共振回路といいます。

L や C の値を自在に変更できる部品を使えば、共振周波数の値も変更でき、そのような共振回路を特に同調回路といいます。＊この回路に、電圧を加えるのではなく電波を浴びせた場合でも、特定の周波数のときに大きな電流が流れます。C の値を調整して共振周波数がたとえば 557MHz の回路を作ればNHKの発した周波数の電流が流れ、545MHz の回路を作れば日本テレビの発した周波数の電流が流れます。
今の若い人は「チャンネルを回す」という言葉の意味が分からないかもしれませんが、昔のテレビはツマミを回してコンデンサーの極板をズラして共振周波数を変更して各テレビ局の電波をキャッチしていました。
　閉じる

共振という言葉は『共振⋅共鳴』項でも出てきましたが、そちらは力学的な共振で、本項で説明したものは電気的な共振です。

また、①式は『RLC直列回路』項で説明した力率が cosφ=1 (φ=0)となるときの式であり、このことから、共振が起こるときというのは電力の効率も良い、ということがいえます。

別解

上記のことは数式を解析することからも導くことができます。

この回路の電流と電圧の関係を示す式は『RLC直列回路』項の⑦式です。

　⑦ →　V_e = I_e\(\sqrt{R^{\small2}+(ωL-\large{\frac{1}{ωC}})^{\small2}}\)

　∴　　I_e = \(\large{\frac{V_e}{\sqrt{R^{\small2}+(ωL-\frac{1}{ωC}})^{\small2}}}\)

ω = 2πf を代入しまして、

　　　　I_e = \(\large{\frac{V_e}{\sqrt{R^{\small2}+(2πfL-\frac{1}{2πfC}})^{\small2}}}\)　　……②

いま、この式の量記号のうち、変数は I_e と f だけです。V_e、R、L、C は固定された値です。このような式は馴染みがないかもしれませんが、I_e が最大になるときは \(\bigl(\)2πfL - \(\large{\frac{1}{2πfC}}\)\(\bigr)\) の中が 0 のとき、つまり、

　　　2πfL = \(\large{\frac{1}{2πfC}}\)

　　∴　　f² = \(\large{\frac{1}{4π^2LC}}\)

　　∴　　f = \(\large{\frac{1}{2π\sqrt{LC}}}\)

であるというのは想像がつくと思います。

グラフ

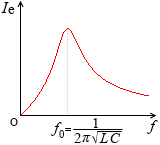②式を簡略化した　I_e = \(\large{\frac{1}{\sqrt{0.3+(f-\frac{1}{f}})^{\small2}}}\)　という式をグラフ描画ソフトに入力して曲線を描いてみると左図のようになります。

山の部分の f の値が　f = \(\large{\frac{1}{2π\sqrt{LC}}}\)　に相当します。これが f₀ です。山は突出して大きくなっています。周波数を変化させていくと、あるところで突然共振が起こるということです。

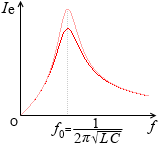上の式の 0.3 の部分をもっと小さい値 0.2 にして　I_e = \(\large{\frac{1}{\sqrt{0.2+(f-\frac{1}{f}})^{\small2}}}\)　として描いてみると左図のようになります。山が高くなります。

0.3 や 0.2 の部分は⑦式における R の部分です。ここを小さくすると山が高くなる、すなわち電流が大きくなるということです。

これらのことはすなわち、

　　　　I_e = \(\large{\frac{V_e}{\sqrt{R^{\small2}+(ωL-\frac{1}{ωC}})^{\small2}}}\)

という式の分母のインピーダンスの部分、

　　　　Z = \(\sqrt{R^{\small2}+(ωL-\large{\frac{1}{ωC}})^{\small2}}\)

が小さいと電流が大きくなる、ということです。