qOCC1

問1～問4に答えよ。

（問1）次の文章中の空欄ア・イに入れる式の組合せとして最も適当なものを、後の①～⑥のうちから一つ選べ。

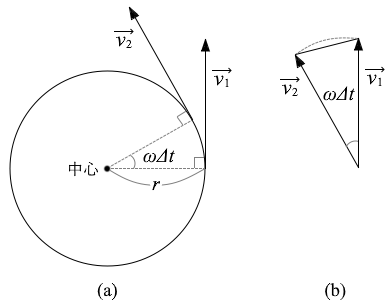
図2(a)のように、半径 \(r\) の円軌道上を一定の速さ \(v\) で運動する電子の角速度 \(ω\) はアで与えられる。時刻 \(t\) での速度 \(\vec{v_1}\) と微小な時間 \(△t\) だけ経過した後の時刻 \(t+△t\) での速度 \(\vec{v_2}\) との差の大きさはイである。
ただし、図2(b)は \(\vec{v_2}\) の始点を \(\vec{v_1}\) の始点まで平行移動した図であり、\(ω△t\) は \(\vec{v_1}\) と \(\vec{v_2}\) とがなす角である。また、微小角 \(ω△t\) を中心角とする弧（図2(b)の破線）と弦（図2(b)の実線）の長さは等しいとしてよい。

図 2

　

① ② ③ ④ ⑤ ⑥
ア \(rv\) \(rv\) \(rv\) \(\Large\frac{v}{r}\) \(\Large\frac{v}{r}\) \(\Large\frac{v}{r}\)
イ 0 \(rv^2△t\) \({\Large\frac{v^2}{r}}△t\) 0 \(rv^2△t\) \({\Large\frac{v^2}{r}}△t\)

　

　

（問2）qOCC2

（問3）qOCC2

（問4）qOCC2

#共テ22本試物理

ア
『等速円運動の速さ』で説明したとおり、半径 \(r\) の円軌道上を角速度 \(ω\) で等速円運動をする物体の速さ \(v\) は

　　\(v = rω\)

であるので、これを変形すると

　　\(ω = \textcolor{yellow}{\underline{\textcolor{black}{\Large\frac{v}{r}}}}\)

です。

（たとえば、半径 \(r\) = 2 [m] の円軌道を速さ \(v\) = 3 [m/s] で周回していれば角速度 \(ω\) は 1.5rad/s です。1秒間に 85.9° くらい回転するスピードです。）

　

イ
『等速円運動の加速度』で詳しく説明したとおり、

　　\(| \vec{v_2} - \vec{v_1} | = vω△t\)

です。

この式に上述の \(ω = \Large\frac{v}{r}\) を代入すると、

　　\(| \vec{v_2} - \vec{v_1} | = \textcolor{yellow}{\underline{\textcolor{black}{{\Large\frac{v^2}{r}}△t}}}\)

です。

（これを \(△t\) で割った \(\Large\frac{v^2}{r}\) が等速円運動の加速度です。）

　

答えは ⑥ です。