光波が境界面で反射するとき、位相がズレるときとズレないときの2パターンあります。（光波が境界面を透過していくときに関しては、位相がズレることはありません。1パターンです。）
屈折率の小さい媒質（たとえば空気）の中を進んでいって、屈折率の大きい媒質（たとえば石鹸膜）に当って反射した光は、固定端反射のごとく位相が \(π\) ズレます（逆転します）。波の山が、反射した瞬間、谷になります。
逆に、屈折率の大きい媒質の中を進んでいって、屈折率の小さい媒質に当たって反射した光は、自由端反射のごとく位相が変わりません。波の山が、反射しても山のままです。
（この原理について、補足ページで大雑把にですが解説しました。）
光波の反射
屈折率 小→大 ： 位相が \(\boldsymbol{π}\) ズレる（固定端反射）
屈折率 大→小 ： 位相は変わらない（自由端反射）
ある媒質の中を光波が進んだときに、実際に進んだ距離に、その媒質の屈折率を掛けたものを光学的距離あるいは光路長といいます。
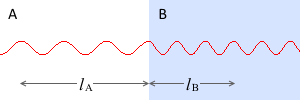屈折率 1.0 の媒質Aから屈折率 1.5 の媒質Bへ進む光波の様子を描くと左図のようになりますが、\(l_{\rm A}\) と \(l_{\rm B}\) は光学的距離としては同じ長さです。どちらも波長3つ分の長さです。波が \(l_{\rm A}\) を進むのに掛かる時間と \(l_{\rm B}\) を進むのに掛かる時間は同じです。
（定規で測ったような）実際の長さとしては、\(l_{\rm A} = 1.5 l_{\rm B}\) です。媒質Bの屈折率を \(n\) とすれば、\(\boldsymbol{l_{\rm A} = nl_{\rm B}}\) と表現できます。
光の干渉の説明においては経路差、光路差という言葉がよく出てきますが、経路差というのは実際の長さの差のことで、光路差というのは光学的距離の差のことです。この2つの言葉は厳密に使い分けなければなりません。空気の場合は、屈折率を 1.0 とみなすことが多いので、そのとき（ヤングの実験や単スリットの実験など）は、経路差=光路差 であり、厳密に使い分ける必要はありません。
光路差というものは、縮んだ波を元通りに引き伸ばして考えたもの、とみなすことができます。経路差を \(2d\)、屈折率を \(n\) とすると、光路差は \(\boldsymbol{2nd}\) です。
シャボン玉の表面や、水面上に広がった油膜の表面が様々な色に映るのは、光の干渉によるものです。透明（半透明）の薄い膜に光が当って反射すると、薄膜上面で反射した波と、薄膜下面で反射した波が干渉するのです。
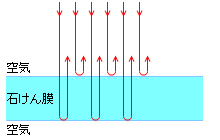光が石けん膜に垂直に当たる場合の反射光について考えてみます。
石けん膜に当たった光は、石けん膜の上面で反射するものと、下面で反射するものとに分かれます。この反射してきた光を石けん膜の真上から観察すると、上面で反射した光と下面で反射した光が干渉し合って、明るく見えたり、暗く見えたりします。 ここでは、石けん膜を透過していく波に関しては考えません。反射波だけについて考えます。
明るく見えるときというのは、上面で反射した光の位相と、下面で反射した光の位相が一致して強め合っているということです。
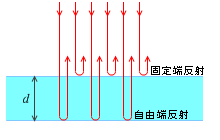
ヤングの干渉実験や回折格子による干渉のときは、光路差が \(mλ\) のとき \(l_1\) と \(l_2\) の光路差が \(λ\) や \(2λ\) や \(3λ\) や \(4λ\) のとき に波が強め合いましたが、今回は、上面で反射した光の位相が \(π\) ズレるので、光路差が \((m + {\large\frac{1}{2}})λ\) のとき \(l_1\) と \(l_2\) の光路差が \(0.5λ\) や \(1.5λ\) や \(2.5λ\) や \(3.5λ\) のとき に波が強め合います。左図のように、石けん膜の厚さを \(d\) とすれば、上面で反射した光と下面で反射した光との経路差は \(2d\) です。つまり、\(2d = (m+{\large\frac{1}{2}})λ\) となるときに、明るくなります。暗くなるときは、\(2d = mλ\) となるときです。
しかしこのままでは間違いがあります。屈折率の大きい石けん膜の中を進む波は波長が小さくなっています。空気中での波の波長を \(λ\) 、石けん膜中での波の波長を \(λ'\) 、石けん膜の屈折率を \(n\) とすると、 \(λ = nλ'\) 、変形して、\(λ' = {\large\frac{λ}{n}}\) です。このような波長で、\(d\) の距離を1往復して上面に到達するとき、(\(m + {\large\frac{1}{2}})λ'\) になっていれば明るく見えるということです。
まとめます。
（垂直に当たる場合）
明るくなる条件 \(2d = {\color{#ccc}(m+{\large\frac{1}{2}})λ'} = (m + {\large\frac{1}{2}}){\large\frac{\lambda}{n}}\)
暗くなる条件 \(2d = {\color{#ccc}mλ'} = m{\large\frac{λ}{n}}\)
\((m = 0,1,2,…)\)
（\(n\) を左辺に移項した場合は以下のようになります）
明るくなる条件 \(2nd = (m + {\large\frac{1}{2}})λ\)
暗くなる条件 \(2nd = mλ\)
\((m = 0,1,2,…)\)
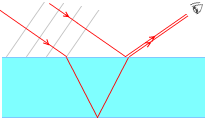左図は、光波の波面の一部が薄膜の上面で反射し、一部が薄膜の中に屈折しながら入射し、下面で反射し、薄膜の上面で2つの光波が干渉し合って観測者の目に届いている場面です。
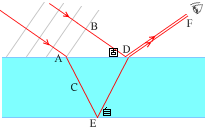B→D→Fと向かう光は固定端反射し、位相が \(π\) ズレます。A→E→D→Fと向かう光は自由端反射し、位相はズレません。
光路差を考えて、明るくなるときと暗くなるときの条件を求めてみます。
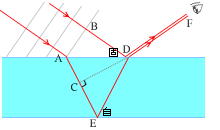経路差は AED - BD ですが、薄膜の屈折率を \(n\) 、空気の屈折率を 1.0 とすると、
光路差は \(n\)×AED - 1.0×BD です。そして、BDとACは光学的距離が同じです。BD = \(n\)×AC です。よって、
光路差は \(n\)×AED - BD = \(n\)×AED - \(n\)×AC であり、
さらに、\(n\)×AED - \(n\)×AC = \(n\)×CED です。
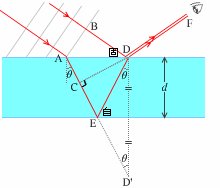そして、左図のように薄膜の下面に対する点Dの対称点を点D'としますと、ED = ED'。よって、CED = CD'。さらに、CD' = DD'cos\(θ\) であるから、
薄膜の厚さを \(d\) とすると、\(n\)×CED = \(n\)×DD'cos\(θ\) = \(n\)×2\(d\)cos\(θ\) = 2\(nd\)cos\(θ\) 。これが求める光路差です。
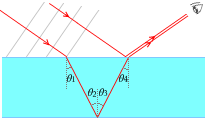角度についてですが、左図の4つの角度が等しくなるのはおわかりでしょうか。\(θ_1\) と \(θ_2\) は錯角なので等しく、\(θ_2\) と \(θ_3\) は反射の法則により等しく、\(θ_3\) と \(θ_4\) は錯角により等しくなっています。
この光路差 \(2nd\cosθ\) が（上の垂直に当たる場合で説明しましたが） \((m + {\large\frac{1}{2}})λ\) となるときに明るくなり、\(mλ\) になるときに暗くなるわけです。
薄膜による干渉
明るくなる条件 \(\boldsymbol{2nd\cosθ = (m + {\large\frac{1}{2}})λ}\)
暗くなる条件 \(\boldsymbol{2nd\cosθ = mλ}\)
\((m = 0,1,2,…)\)
この式において \(θ = 0\) すなわち垂直のとき、\(\cosθ = 1\) となり、これはつまり、
明るくなる条件 \(2nd = (m+{\large\frac{1}{2}})λ\)
暗くなる条件 \(2nd = mλ\)
ということであり、上の垂直に当たる場合の式のことであります。
また、この式により、しゃぼん玉の表面が様々な色を映す原理を説明できます。
まず、しゃぼん玉は球体なので屈折角 \(θ\) が様々な値をとり、また、膜の厚さ \(d\) も均一ではないので、上式の左辺 \(2nd\cosθ\) が様々な値をとります。よって、右辺の \(λ\) も様々な値をとります。波長 \(λ\) の違いというのは可視光線でいうところの色の違いのことですので、しゃぼん玉の表面は様々な色を映す、ということになります。でもこれは、様々な波長を含んだ白色光（太陽や白熱電球の光）を当てた場合の話です。1種類の波長（色）しか含んでいない単色光（レーザー光などの人工的な光）を当てた場合は、1種類の色の縞模様が現れます。